Se dobbiamo calcolare il quadrato di un numero di 2 cifre che termina per 5 l'operazione è semplicissima:
Per esempio se voglio calcolare il quadrato di 35, le ultime cifre sono 25 e le prime le ottengo moltiplicando 3*(3+1)=3*4=12. Quindi il quadrato di 35 è 1225.
Si fa prima a farlo che a dirlo.
Questo è un caso particolare della moltiplicazione di due numeri che distano in egual misura ma con segno opposto da un numero che termina per 5 . In questo caso si ha:
Si fa prima a farlo che a dirlo.
Questo è un caso particolare della moltiplicazione di due numeri che distano in egual misura ma con segno opposto da un numero che termina per 5 . In questo caso si ha:
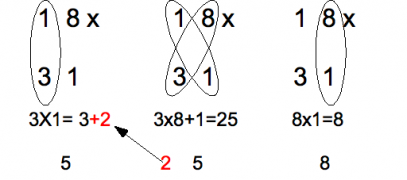
Facciamo un esempio 33*37. Entrambi distano di 2 unità da 35. Il risultato della moltiplicazione l'ottengo facendo 3*4=12 e 3*7=21 : 1221. Da notare che sia per le cifre più significative che meno significative dobbiamo considerare gruppi di 2 cifre come risultato.
Ad esempio 19*11= (2*1)|9*1=02|09=209 . Oppure 29*21=609
Ad esempio 19*11= (2*1)|9*1=02|09=209 . Oppure 29*21=609
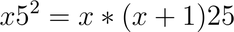
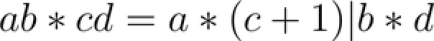
 RSS Feed
RSS Feed
