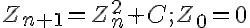Insieme di Mandelbrot [DRAFT]
Secondo Progetto Obbligatorio.
E' l'insieme dei numeri complessi C per cui
non diverge.
Dato che OGNI PUNTO è indipendente da ogni altro il problema è "embarrassingly parallel" e può essere parallelizzato sia come divisione di dati che come divisione di compiti. Quella che vogliamo è una soluzione basata sulla divisione di compiti dato che la divisione di dati è stata già affrontata nel caso del Game of Life.
Prima di generarlo voglio farvi fare un compito più semplice ma correlato con questo, l'integrazione "Montecarlo".
Come fare a calcolare numericamente l'area di una figura irregolare ? Se ho una regola in basa alla quale posso stabilire se un punto appartiene o no alla figura irregolare posso circondarla con una regolare di area nota, estrarre N punti a caso e contare quelli che vi cadono.
Il rapporto fra il numero totale di punti estratti e quelli che cadono nella figura in esame è una misura del rapporto delle due aree e tenderà a questo per grandi N. Si dimostra che l'errore commesso è proporzionale a 1/sqrt(N).
L'esempio classico che si da (anche in Wikipedia) è quello del rapporto fra l'area del cerchio di diametro unitario e il quadrato di lato 1: Pi/4.
Fare un programma che estrae N coppie di numeri a caso tra 0 e 1 che chiamiamo (x,y) e conta i punti tali che x^2+y^2<=1 è un problema classico e altamente parallelizzabile. ( vedi figura sotto)
L'estrazione di numeri a caso in ambito di programmazione parallela è un argomento che merita una trattazione a parte. Una libreriaportabile e ricompilabile è la SPRNG.
In questo caso dedicate un PE a generare i numeri e a fare da SERVER per gli altri PE che saranno CLIENT ( o Master/Slave se preferite).
Dato che OGNI PUNTO è indipendente da ogni altro il problema è "embarrassingly parallel" e può essere parallelizzato sia come divisione di dati che come divisione di compiti. Quella che vogliamo è una soluzione basata sulla divisione di compiti dato che la divisione di dati è stata già affrontata nel caso del Game of Life.
Prima di generarlo voglio farvi fare un compito più semplice ma correlato con questo, l'integrazione "Montecarlo".
Come fare a calcolare numericamente l'area di una figura irregolare ? Se ho una regola in basa alla quale posso stabilire se un punto appartiene o no alla figura irregolare posso circondarla con una regolare di area nota, estrarre N punti a caso e contare quelli che vi cadono.
Il rapporto fra il numero totale di punti estratti e quelli che cadono nella figura in esame è una misura del rapporto delle due aree e tenderà a questo per grandi N. Si dimostra che l'errore commesso è proporzionale a 1/sqrt(N).
L'esempio classico che si da (anche in Wikipedia) è quello del rapporto fra l'area del cerchio di diametro unitario e il quadrato di lato 1: Pi/4.
Fare un programma che estrae N coppie di numeri a caso tra 0 e 1 che chiamiamo (x,y) e conta i punti tali che x^2+y^2<=1 è un problema classico e altamente parallelizzabile. ( vedi figura sotto)
L'estrazione di numeri a caso in ambito di programmazione parallela è un argomento che merita una trattazione a parte. Una libreriaportabile e ricompilabile è la SPRNG.
In questo caso dedicate un PE a generare i numeri e a fare da SERVER per gli altri PE che saranno CLIENT ( o Master/Slave se preferite).
Fate contare dai client i punti che cadono nel cerchio e alla fine calcolate 4*il rapporto con il numero di punti totali estratti. Se tutto va bene dovreste ottenere Pi. Il sorgente si una prima versione di questo programma lo trovate qui.
| easybmp_variousbmputilities.h | |
| File Size: | 1 kb |
| File Type: | h |
| easybmp.h | |
| File Size: | 2 kb |
| File Type: | h |
| easybmp_datastructures.h | |
| File Size: | 2 kb |
| File Type: | h |
| easybmp_bmp.h | |
| File Size: | 2 kb |
| File Type: | h |
| mandelbrot_core.cpp | |
| File Size: | 1 kb |
| File Type: | cpp |