Quan'ero bambino non avrei mai immaginato di poter fare le moltiplicazioni con un disegno. Ma la vita è bella perché s'impara sempre qualcosa. Questo l'ho imparato ieri sera.
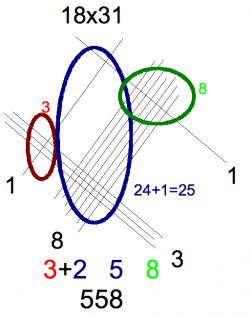
Per fare 18x31 ho disegnato la prima linea in alto a sinistra, le 8 linee in basso da sinistra a destra, le 3 linee in basso da destra a sinistra e la linea in alto a destra. Poi ho contato gli incroci: i 3 a sinistra, cerchiati in rosso nel disegno, il gruppo centrale di 25, in blu, e gli 8 a destra in verde. Fatto. L'ultima operazione è sommare il 2 der 25 al 3, un riporto ottenendo le cifre del risultato: 558. Confesso che ho controllato con la calcolatrice perchè non ci credevo nench'io. Bello eh ?
 

Qual'è la tabellina del 26 ? Allora 26 52... 78... Uffa ma quanto ci metto ! Se vi dicessi che c'è un metodo che ci permette di calcolarla in pochi secondi ? Potete anche non crederci ma esiste.
Prima di calcolarla però dobbiamo imparare che cosa sono e come si calcolano i numeri vincolo.
In Matematica Vedica lavoriamo con le singole cifre. Prima di dargli una "definizione formale" diamo una definizione algoritmica dei numeri vincolo le cui cifre possono essere singolarmente positive o negative ma sempre in valore assoluto <=5. Per ora ci basta sapere che questi numeri saranno la chiave per calcolare qualunque tabellina in brevissimo tempo.
Vediamo un esempio supponiamo di voler calcolare il numero vincolo di 3745
Osservo che il 7 è l'unica cifra > 5. Quindi applicando i 2 sutra visti prima:
1) Di uno innalza quel che sta d'innanzi
2) Da nove tutti e l'ultimo da dieci.
Aumento di 1 il 3 perchè sta davanti al 7
Sottraggo 10 da 7 perchè 7 è l'unico e quindi l'ultima cifra di un gruppo di cifre >5.
Lascio invariate le altre cifre perchè <=5.
Ottengo:
4(-3)45  Notate il segno - applicato solo alla cifra 3.

E se volevo il numero vincolo del 26 ?
Dimostrate che con le regol precedenti ottengo 3(-4).
Come posso usare questo numero per calcolare la tabellina del 26 ?
Scriviamoli incolonnati:
   3 -4
   2  6  e non faccio altro che SOMMARE cifra a cifra. Ottengo:
   5  2  che è 26*2 ora sottraendo -4 a 2 devo prendere un prestito dall'altra colonna e quindi:
   7  8 
1 0  4
1 3  0  ancora un'altro prestito
1 5  6
1 8  2 ultimo prestito
2 0  8
2 3  4
2  6  0 Fatto !

Facendo in questo modo ho ridotto la complessità delle somme e aumentata la velocità di calcolo.
E la tabellina del 3745 ?

4   -3   4   5
3   7    4   5   5+5=10 quindi devo fare un riporto di 1

7   4    9    0
11 2    3    5  Controllate che questo sia proprio 3745 x 3 e finite la tabellina...

e se ho 5890 ? Come calcolo il suo numero vincolo ? Se aumento di 1 il 5 ottengo il 6 che non può apparire e quindi : ci metto uno 0 davanti e tratto quel 5 come se fosse una cifra "grande"

0 +1 =1
5 - 9 = -4
8 - 9 = -1
9 -10 = -1
0  rimane invariato.
Controllate voi.... con carta e matita si fa prima !
   1   -4   -1   -1    0
   0    5    8    9     0
   1   1     7    8     0
   1   7     6    7     0   
   2   3     5    6     0
   2   9     4    5     0
   3   5     3    4     0
   4   1     2    3     0
   4   7     1    2     0
   5   3     0    1     0
   5   8     9    0     0

L'ho stesa a mano neanche fossi una sfoglina in meno di un minuto !

Vi segnalo  questa pagina http://liberius1776.wordpress.com/2008/08/02/vinculum-numbers/
che contiene moltissime altre informazioni sui numeri vincolo...... che in effetti avevamo già usato nelle sottrazioni.....

Sapete fare le sottrazioni ?
Perbacco Certamente si !
E quanto tempo ci mettete a fare
11111 -
 1792 =
 9319 ?

Io che sono alle prime armi con la matematica Vedica ci ho messi circa 5 secondi e potevo sicuramente far meglio ! E potete farlo anche voi ! Come ho fatto ? .... Beh cerco di spiegarvelo con quello che ho capito e se qualcuno di voi ha commenti o vuol correggermi è BENVENUTO !
Vi assicuro che è MOLTO più facile a farsi che a dirsi !
La Matematica Vedica è basata su dei SUTRA ovvero degli aforismi che vengono applicati alle CIFRE dei numeri dell'operazione che dobbiamo fare.
In questo caso si applicano 2 SUTRA che traduco molto liberamente dall'inglese (scusate non conosco il sanscrito) cercando di dargli un minimo di metrica.
1) Di uno innalza quel che sta d'innanzi
2) Da nove tutti e l'ultimo da dieci.
Che vogliono dire e come si applicano ? Guardiamo le cifre della sottrazione proposta:
Nel sottraendo le cifre 1792 sono più grandi o uguali a quelle del sottraendo, potremmo scriverlo anche come 01792 e in questo caso lo 0 che sta davanti a tutti è una cifra più piccola di quella del sottraendo. La regola che ho imparato è che
A ) Devo applicare 1) a questa cifra (è difronte a un gruppo di cifre più alte) e sottrarla alla corrispondente cifra del minuendo.
B) Sottraggo da 9 le altre cifre e le sommo cifra per cifra a quelle del minuendo salvo che per l'ultima cifra ove uso 10 al posto di 9.
In pratica ho fatto:
1 - (0+1) = 0
1 +(9- 1) = 9
1 +(9- 7) = 3
1+ (9 -9) = 1
1+(10-2) = 9
Riducendo questa sottrazione in una serie di operazioni semplicemente calcolabili a mente si aumenta moltissimo la velocità di calcolo ! E' la differenza fra processori RISC e CISC tante operazioni semplici sono più rapide di una complessa !

Bene e ora un esempio un pizzichino più complesso:
423462 -
187175

AAALT.... un attimo prima che partiate in quarta notate quell' 1 centrale nel sottraendo. Mi divide le cifre del sottraendo in due gruppi ciacuno dei queli è formato da due cifre più alte di quelle del minuendo e una innazi a loro...... avrete già capito che in questo caso e in tutti i casi simili i sutra si applicano due volte. Quindi a tutto gas possiamo fare a mente:
Primo gruppo di cifre:
4 -(1+1) =2
2 +(9-8) =3
3 +(10-7)=6   10 perchè è l'ultima cifra del primo gruppo
Secondo gruppo di cifre:
4-(1+1) =2
6+(9-7) =8
2+(10-5)=7    

236287  e chi ha preso il calcolatore sta ancora pigiando i tasti ! (Tiè !)
Notate che sono TUTTE operazioni entro 9 e non abbiamo mai fatto neanche un riporto !
Con le regole che avete imparato verificate che:
101210-
  10701=
  90509
NB.: In un gruppo di cifre quando c'è n'è solo una è ovviamente l'ultima e quindi uso 10 nel sutra 2.
Tutto ok ? Bene .....e ora fate magiare la polvere ai vostri Prof.!

Tanto per fare un piccolo esempio se vi chiedessero a bruciapelo: Quanto fa 27 x 11 ?
Immagino che mentalmente fareste : 270+27 = 297 .... OK Vero ma c'è un metodo più semplice
Scomponendo il 27 nelle sue due cifre le cifre del risultato sono 2 (2+7) 7 ovvero se chiamiamo le cifre A e B il risultato in cifre è A (A+B) B.
In effetti vedo subito che i due metodi sono equivalenti se scrivo 270+27 in colonna.
                                                                                 270 +
                                                                                   27
                                                                                 297 
Se A+B >= 10 basta aumentare la prima cifra col riporto di 1:
39 x 11 = 3 (3+9) 9 = 3 (12 ) 9 = (3+1) 2 9 = 429
Dal punto di vista mentale questo metodo è un proceso rapidissimo.
E se il numero da moltiplicare avesse molte cifre ?
ABCDE x 11 = A (A+B) (B+C) (C+D) (D+E) E
Anche in questo caso se una delle somme è >= 10 aumentate di 1 la cifra a sinistra e partite a calcolare le somme da quella più a destra.
12345  x 11 = 135795
PROVATE ESEMPI E FATELI A MENTE.
POI SU UN PEZZO DI CARTA.
La vostra mente è molto più potente di qualunque calcolatore ! Sfidate gli amici e i vostri prof. !

Salve Ragazzi ! Devo proprio dirlo non si finice mai d'imparare! Recentemente ho saputo l'esistenza di un sistema matematico indiano chiamato Vedico col quale operazioni per noi difficilissime vengono svolte in modo estremamente semplice.
L'idea di reimparare la matematica da un'altro punto di vista mi affascina e mi piacerebbe condividerla con voi. Non so se potrò postare regolarmente..... in questo campo, come in molti altri, sono uno studente anch'io.
Comincio col riportare questo link:
http://www2.polito.it/didattica/polymath/htmlS/argoment/Matematicae/Dic_07/Vedica.htm
che contiene molte informazioni in italiano.