Prima di parlare di condensatori abbiamo affrontato il caso di due sfere conduttive con raggi r<R allo stesso potenziale.
Da cui si ottiene:
Quindi la sfera piccola ha meno carica e minor capacità ma questo non vuol dire che ci sia meno campo. Infatti se vado a calcolare la densità di carica devo dividere per il raggio al quadrato e quindi:
Quindi..... il campo elettrico intorno a una punta è molto più alto che nel resto di un conduttore.
Abbiamo quindi parlato un condensatore a piatti piani paralleli. Ricordando che il campo elettrico generato da un disco uniformemente carico è:
Abbiamo quindi parlato un condensatore a piatti piani paralleli. Ricordando che il campo elettrico generato da un disco uniformemente carico è:
Dato che in un condensatore abbiamo due piani opposti con cariche opposte il campo all'interno raddoppia (... verificatelo con un disegnino ....e fuori ?) chiamando d la distanza fra i piani ed A la loro area posso integrare il campo in modo da ottenere la differenza di potenziale:
Da cui è immediato ricavare la famosa formula per la capacità:
A questo punto abbiamo ricavato le espressioni per condensatori in parallelo ( le capacità si sommano ) e in serie ove invece si sommano l'inversi:
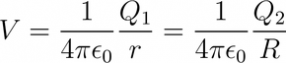
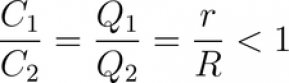
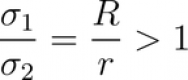
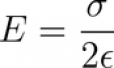
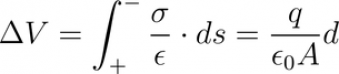
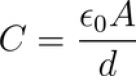
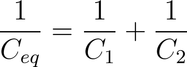

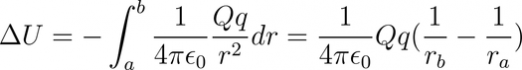
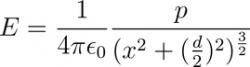
 RSS Feed
RSS Feed
